© Copyright 2005
All rights reserved.
Permission for reproducing is required.
FERMAT’S LAST THEOREM: THE PROOF RESULTING IN CALCULATING ALGORITHM.
by Ivan M. Obushenko, Ph.D.
E-mail: obush@estart.com
Printed on March 8-10, 2005
Summary
The new approach for consideration of the legendary Fermat’s Last Theorem has been developed. One advantage has been received from proposed consideration: the calculating algorithm for PC – “ Obushenko-Fermat MachineÔ ” making the calculation process by fully automated and expendable unlimitedly . The “byproduct” of calculation is a finding of all integer triads fulfilling to the Pythagoras Theorem.
Fermat’s Last Theorem
For integers a, b, c, and n>2 an + bn ¹ cn .
THE PROOF
The current consideration is substantially based on following Lemma expressing my basic idea led me forward.
Lemma. For any three numbers a, b, c, for which a + b > c some triangle can be constructed.
That Lemma arisen from the everyday experience and can’t be proved in principle on my opinion. So it rather Axiom than Lemma . Indeed, let’s make a drawing for a, b < c :
a m b
Drawing 1.![]()
![]()
![]()
c
Case#1. What,
if a + b < c
Let’s put for clarity |a|<|b|<|c|, where |a|=mod a .
For a + b < c and a + b +m = c (according to the Drawing 1.) and assuming all numbers to be positive one can conclude:
a2 + b2 < c2 =[(a + b)+m]2 = a2 + b2 + 2ab + 2(a + b)m + m2. (1)
By multiplying that inequity (1) by c we will obtain
a2c + b2c < c3 (2)
and by observing that a3< a2c and b3< b2c we can conclude that
a3
+ b3 < c3 .
By applying the Mathematic Induction Method we now can easily prove that for any
a + b < c from fulfillment of inequity an-1 + bn-1 < cn-1 the following one will be true:
an
+ bn < cn (3)
like it was
for (1) and (2).
What if one or two or all three integers will be negative ?
If the
smallest is negative. Then for even
power n=2k we’ll get obviously an
+ bn < cn because (-a)2k=a2k
for k≥1 and we are getting back to the already proved expression
(3) above.
For the odd power n=2k+1
-an
+ bn < cn (4)
because we set from beginning |a|<|b|<|c|, where |a|=mod a.
If the intermediate is negative (b<0). Then for even power n=2k we’ll get obviously
an
+ bn < cn because (-b)2k=b2k
for k≥1 and we are getting back to the expression (1).
For the odd power n=2k+1
an
- bn < cn (5)
because we set from beginning |a|<|b|<|c|, where |a|=mod a.
If the
biggest is negative. Then again
for even power n=2k we’ll get obviously an
+ bn < cn because (- c)2k=
c2k.
For the odd power n=2k+1
b2k+1 + a2k+1 > - c2k+1 (6)
on the left we have the positive number, while on the right side of inequity
.
Case#2. What, if a + b = c
Let’s put for clarity |a|<|b|<|c|, where |a|=mod a and all integers are positive (>0).Then
a2 + b2 < c2 = (a + b)2 = a2 + b2 + 2ab (7)
and by applying to the expression (9) the same operations as to the case (1) above we are obtaining for a + b = c
an
+ bn < cn . (8)
In power of similarity condition (1) to condition (9) all possible combinations for the negative integers considered in Case #1 will be merely all the same. That’s why I don’t repeat it here: it was promised the enjoyable proof – not the boring one. J
Case#3. What,
if a +b > c
(some triangle can be
constructed)
Well, the good news is that this case is the last one: no more relationships between a, b, c are available (except a sign of course). One more good news is the number of different type of triangles is finite and not too much. J
Let’s start from the simplest: a=b=c , the equiangular triangle. Obviously a+ a>a and
2(an)>an
when an >0; or 2(an)<an
when an <0 for every n ≥ 2.
The next obvious thing is a<b=c , i.e. one of the possible isosceles triangles. Obviously a+ b>c and an+ bn > bn when an >0 and bn >0; or an+ bn < bn , if either an<0 or both an, bn <0 for every n ≥ 2.

a’
b’ Drawing. 2
a b

c
As we see
from Drawing. 2 the three type of triangles is representing the rest of possible
relationships between integer a,b,c .
Right-angled
triangle.
The key point here is the right-angled triangle of course, for which
a2 + b2 = c2. (9)
Again as usually let’s put for clarity |a|<|b|<|c|, where |a|=mod a .
Let’s multiply the expression (10) by c :
a2c
+ b2c=
c2c. (10)
However such as a3< a2c and b3< b2c we can conclude that
a3 + b3 < c3 (11)
and by
applying further the approach of Mathematic Induction we will come to
conclusion (3) again: an + bn
< cn .
Certainly because of the inequity (11) taking place the consideration for negative integers will be all the same as in Case#1 and #2 : it’s still no chance for equity (one can check it out).
Obtuse-angled triangle. Oh, this is a simple one after the right-angled triangle was done right now: just take a look on Drawing. 2. Does anyone want a detailed consideration ? I’m simply writing down the obvious results:
a2
+ b2 < c2 , a3 + b3
< c3 and an
+ bn < cn (12)
plus the inequities (5), (7) and (8), if some from integers a,b,c happen to be negative and referring the readers to the corresponding place in Case#1.
Scalene triangle. This case is the most complicated. From Drawing. 2 the first what we see is
a2 + b2 > c2. (13)
The approach of multiplying by c and then replacing the members of inequity on smaller
values won’t be applied here. So, even for n=3 we can not make any general conclusion.
The direct calculations for some well known numbers demonstrate that direction of inequity sign will depend on absolute values of a,b,c and n .
For example, for n=3 , a=4, b=5, c=7 ( something close to Pythagoras’ triangle 32 +42=52 )
43 + 53 =280 < 73 =343, while 42 + 62 = 52 > 72 = 49 as it should be according to the general inequity (12). But as soon as a,b,c each becomes larger than 10 then inequity will have the same direction as for square power by starting already from cube:
103+113=2331>133 =2197.
Let’s take one more look at another Pythagoras’ triangle 62 +82=102.
For closest scalene triangle 72+82=113>102, while 73+83=855<103 and even
7100 + 8100=2.037*1090 < 10100=100*1090 and the difference is just increasing with increasing n.
From other side: 103+113 =2331>123=1728 but <133=2197.
So, generally saying for scalene triangle the direction of inequity can take both sides:
< and >.
Nevertheless the geometric images is not only help us to embrace and systematically consider all possible cases for Fermat’s theorem but now it gives us an opportunity to develop a general strategy to write down some expressions allowing us to deduce some useful conclusions concerning on verification of Fermat’s Last Theorem.
In attempt to build up some systematic way for calculations we may use our experience obtained during the current consideration. Indeed, let’s find out for any given c a pair of a and b, for which an + bn = cn . As we found out by using Drawing. 2 the possible solution, if it exists at all can be only “between” right and scalene triangle built on given c.
The easiest and certain way is to start out of the equiangular triangle having sides equal to
c-1, c-1 and c (at the beginning of the Case#3 consideration it was shown that it makes no sense to get anything useful in isosceles triangles with b=c.J)
δ = (c-1)n + (c-1)n - cn = 0. (14’)
Of course it will be ¹0 but we are looking for δ=0 and therefore we’ll make our next step:
δ = (c-1)n + (c-2)n - cn = 0 then δ = (c-1)n + (c-3)n - cn = 0 and so on until inequity will change its direction or until (c-t)=1.
Then we will put δ = (c-2)n + (c-2)n - cn = 0 and check out all possibilities to get δ=0.
Well, all that is god for computer but not for mathematics.
For mathematics we should make a suggestion:
(c-s)n + (c-t)n = cn, (14)
i.e. there are some s and t , for which the equation (14) is correct.
Basically the parentheses can be expanded by means of Newton’s binomial formula however without loosing commonness and for better visibility I’ll make it for n=3 and 4, and for s=1, t=2 only:
(c3 – 3c2 +3c –1) + (c3 - 6 c2+12c –8) - c3 = 0 (15)
(c4-4c3+6c2-4c+1) + (c4-8c3+24c2-32c+16) - c4 = 0. (16)
Thus the consideration of Fermat’s Last Theorem is reduced to the problem of the polynomials comparison. As it is stated in the polynomials theory: “The two polynomials are equal then and only then when the pairs of their corresponding members are equal.” It is introducing by definition what means it is free of proof necessity.
As we see on equations (15), (16) after the corresponding contraction of c3 in (15) and c4 in (16) staying alone with the appropriate ones in either of parentheses there is no chance for those two parentheses to be equal. even at s=t because of specificity (or originality) of general equation (14) and in force of definition for polynomials equity. Well, this was a good chance to put a big fat point in Fermat’s Last Theorem history. But as justifiably remarked to me one of our mathematic fellow ( I am not naming him since I don’t have his approve on it): the polynomials could not be equal, while sometime their values do – like the Pythagoras equation (now it’s my turn to make remarks: no more examples are available doesn’t it ? J). That’s why below I’ll try to use that point for further development.
If we apply the theory of limits to the expressions (15), (16) we will see that at given n>2 when c→∞ then lim δ→∞ too (exprs. (14’, 15, 16). It means: the bigger c, the less chances that the curves in parentheses would intersect at all. When c→0 then lim δ→Ω
Similar conclusions can be made for given c and growing power n.
Thus once an inequity δ (14’) turns its direction its most the like that it never get back.
For better understanding the nature of intersecting of curves, which is not continuous let’s consider again the case
(c-s)2 + (c-t)2 = c2
(c-s)2 = c2 - c2 +2ct – t2 = 2ct – t2. (17)
This is possible intersection of square “parabola” and a straight “line”.
Example: s=2, t=1 and details are on Drawing 3. below :
(c-1)2
+ (c-2)2 = c2
(Some general remark concerning on Drawings 3, 4, 5 should be made: during the Words’ file transformations the parabolas (c-s)2k on Draw.3 and 5 spontaneously move up, while it should touch the axe “c” at c=s of course. Sorry for inconvenience).
y


![]() (c-s)2 t/2<s
(c-s)2 t/2<s

![]() Drawing
3.
Drawing
3.
t/2>s
(c-s)2=y=2ct – t2
![]()
![]()
![]()
![]() s (c=0;
y= – t2 )
s (c=0;
y= – t2 )
t/2 c (y=0; c= t/2)
-t2 t/2 c0
![]() -t2
-t2
![]()
y
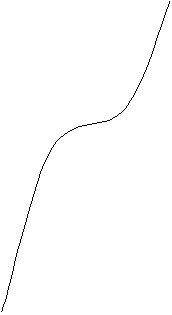

![]() (c-s)2k+1
(c-s)2k+1
+mc2k -…+t2k+1 Drawing 4.
for n=2k+1
![]() y = (c-s)2k+1 = +mc2k -…+t2k+1
y = (c-s)2k+1 = +mc2k -…+t2k+1
s c
 Drawing
5.
Drawing
5.
![]() (c-s)2k
(c-s)2k
 s2k c2k-1+…-
t2k for n=2k
s2k c2k-1+…-
t2k for n=2k
y=(c-s)2k = +mc2k-1 -…-t2k+1
![]() s c
s c
-t2k-1
As we see at the Drawing 3. for the same functions (17) dependently from parameters s and t , which physically just changing the long of smaller triangle sides built on basis of given c (Drawing 2) the necessary conditions for intersection may be created (when t/2<s) or may be not created (when t/2>s).
I said “necessary conditions” because the visible impression like on Drawing 3 does not guarantee yet that the curves indeed intersect because they are not continuous in differ of real numbers. This constitutes the magic of integer numbers and that’s why it is possible to establish the necessary conditions only, not the sufficient ones, which would be the proof of Fermat’s Last Theorem.
Further I will examine a possibility (14’): whether δ = (c-1)n + (c-1)n - cn = 0. For example, if we assume for n=3 and that there are all three solutions for integers and expand
(c – x)(c – y)(c – z) = c3
– (x + y + z)c2 + (xy + xz + yz)c – xyz =
= c3 – 3(s+t) c2 +3(s2 + t2)c – (s3+t3)=0 (18)
and then compare coefficients with the Newton’s ones from expression (14) we will receive the hole system of equations or conditions for (x+y+z), for (zy+xz+yz) up to x*y*z=s3+t3:
x+y+z=3(s+t)
xy + xz + yz=3(s2 + t2)
xyz= s3+t3 (19)
or in
case of degenerated solutions when x=y=z
3x=3(s+t)
3x2=3(s2 + t2) (20)
x3= s3+t3
The system of equations (20) is obviously incompatible: if the first equation is right, then the second will be wrong. Thus the sum or differences of two or three polynomials can never give the full power of that one (polynomial) including n=2. But one can ask: “What about the Pythagoras theorem?” Well, the answer will be: “It falls into general system similar to (19).
Indeed, 52=42+32 can be represented as c2=(c-1)2+(c-2)2 then δ = (c-1)n + (c-2)n - cn =c2-6c+5=(c-5)(c-1) and thus x+y=2(s+t)=6 and xy=s2+t2=12+22=5 where x=1, y=5, s=1, t=2. It’s very important to point out here that the Pythagoras theorem was NOT proved here! We knew in advance the suitable set of 4 numbers! Well, so how someone expects to prove incomparably more complicated system (19)? Otherwise saying the “proof” was done by means of direct numeric calculation! That’ what I will do too for Fermat’s.
Now, if we get back to the system (19) one could conclude the well known condition: possible solution(s) could be (but not should be!) a divisor of sum of the two cubes, which should also fulfill to the second equation of system (19) in order to be a solution (so one of those conditions may be considered as the necessary one, while another becomes the sufficient one) . Can anybody prove it? I’d wonder. But even if somebody could, then for the δ in equation (14’) will be one more possibility to turn into “0”: to be represented similar to one of the follow
(c-x)(c2-c-1)= c3 – 3(s+t) c2 +3(s2 + t2)c–(s3+t3)= 0 (21)
where (c2-c-1) is just one of the many possible undividable squares, which can be considered only for every particular case. And because of it the Theorem can not be proved as a general claim or statement because it is impossible even to write down something like the system (19) not saying about the possibility to prove it. Or one should prove first that ANY δ = (c-1)n + (c-1)n - cn can be represented as a product of n cofactors of the first degree and then secondly to prove the whole system - like the (19) one - to be right. Well, the first requirement sounds obviously wrong from beginning.
Thus I showed above that a condition of existence for the sum of two cubes (or other powers) to have or not to have a divisor can be accepted only as the necessary condition, while the sufficient condition(s), which could make the Theorem provable CAN NOT BE SET UP IN PRINCIPLE. This is the main cause why the Theorem was not been proved for over 350 years.
And hence I propose the “Obushenko-Fermat Machine™”, which can make the calculations by fully automatic excluding any gaps or arithmetic mistakes.
DISCUSSION
What was seen above reminds me more and more an attempt to catch very small baby size fish by using the net for playing soccer or volleyball. The results can be improved little bit by substituting the net with one for playing a ping-pong: this is what Pythagoras equation does for integers. And the larger c and n the less chances on success obviously: the holes are getting larger and larger…
From that point I think the Fermat’s Last Theorem is a problem for probability & statistics guys rather than for the numbers theory ones. J
CONCLUSIONS
A new approach for considering the Fermat’s Last Theorem had been disclosed above and shown to be useful. The Theorem had been considered in a comprehensive manner.
It was found the ranges of a, b, c , for which the Theorem has been proved strictly and unambiguously
(a + b)<c and (a + b)=c (22)
It was circled the range of a and b for every given c where the solution(s) for Fermat’s equation could be, if they would exist at all . That “circle” is given by the following inequities
c2<
a2+b2<2c2 |c|<|a+b|<2|c|
(23)
,
where |a|=mod a .
During the process of consideration a series of boundaries and limitations were established.
Specifically it has been shown that: “If we apply the theory of limits to the expressions (15), (16) we will see that at given n>2 when c→∞ then lim δ→∞ too (expressions (14’, 15, 16). It means: the bigger c, the less chances that the curves in parentheses would intersect at all or their sum would have intersect with the axe “c”, i.e. to be equal to zero. When c→0 then lim δ→Ω”.
There was found some relationship (14), which was useful because of availability to turn it into computers’ algorithm; its functioning was partially described in Case#3 of the consideration. Based on the current consideration that algorithm called the “Obushenko – Fermat Machine” ™ made able to perform the fully automated verification of the Theorem for the remaining range of variables, for which the traditional methods as it was shown could not give the numeric results and thus made the proof to be completed.
Thus the undertaken consideration ultimately allowed TO PROVE the Fermat’s Last Theorem TO BE RIGHT:
for
the integer numbers at n>2 an + bn ¹ cn
.
The values of algebraic sums of any two polynomials of the same power n>2 with integer coefficients and integer variable, while the coefficient at the members with major power is equal to 1, constitute the non-intersecting sets of integer numbers with the sets of the values of anyone third similar polynomial of the same power.
Any two polynomials with integer coefficients and variables and having their major powers n>2 differing by 1 constitute the non-intersecting sets of integer numbers by their values.
Publishers of books on Mathematics should consider an option to provide larger margins on the pages.
References
1. Dictionary of Science. Edited by Peter Lafferty & Julian Rowe. Brockhampton Press, London, 1997. ISBN 1 – 86019 – 501 – 6.
2. Fermat’s
Last Theorem. Article by: J J O'Connor &
E F Robertson, February 1996.
WebPage. http://www-history.mcs.st-andrews.ac.uk/HistTopics/Fermat's_last_theorem.html
3. "IS FERMAT'S LAST THEOREM PROVEN?". Article by: James Constant , 2002.
WebPage. http://wiles.coolissues.com/wiles.htm